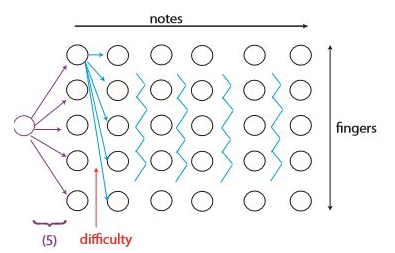
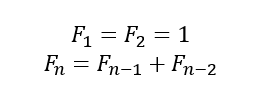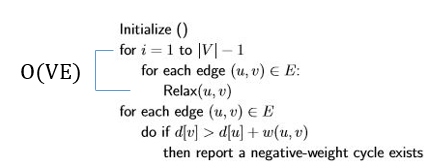BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 복습 ⁉️ 동적 프로그래밍의 5단계 하위 문제 정의하기 ⇒ 하위 문제의 개수 세기 (해법의 일부분을) 추측하기 ⇒ 선택지의 개수 세기 하위 문제의 풀이 연관짓기 ⇒ 하위 문제당 시간 계산 재귀+기억 또는 DP 테이블을 상향식으로 만들기 ⇒ 시간 = 하위 문제당 시간·하위 문제의 개수 하위 문제가 비순환적인지/위상학적 순서인지 확인하기 원래 문제 풀이 ⇒ 추가 시간 필요 : 하위 문제의 풀이 또는 하위 문제들로 조합하여 풀기 ✔ 2종류의 추측 2&3단계에서 어떤 하위 문제를 사용할지 추측 (피보나치를 제외하고 모든 동적 프로그래밍에서 사용) 1단계에서 정답 구조에 대해 더 많은걸 기억하거나 추측하기 위해 ..