ㅇㅅㅎ

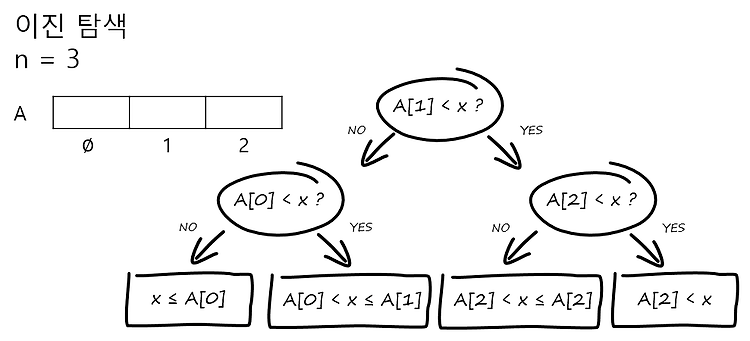
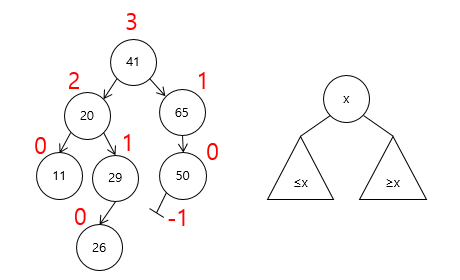
BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 복습 √2 를 백만 자릿수까지 계산 |√a|를 뉴튼 방법을 이용하여 계산 위의 결과들이 실제로 이차적 수렴의 성질인지 알아보기 위하여 뉴턴법의 오차를 살펴보겠습니다. ✔ 뉴턴법의 오차 분석 전체적으로 보았을 때 알 수 있는 것은 오차에 대한 아래의 식입니다. 분모 부분의 (1+εn)에서 n이 계속해서 커질수록 εn은 예상했던 대로 0에 가까워집니다. 그래서 (1+εn) 값은 1이라고 할 수 있고 결국 오차값이 이차적 수렴의 성질을 가진다고 할 수 있는 것입니다. 굉장히 작은 값이지만 매 반복마다 제곱값으로 작아지는 것입니다. 만약 0.01이 가장 처음의 εn 값이라고 한다면 (εn)^2은 0.0001이 ..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 무리수 : 피타고라스는 정사각형의 대각선의 길이와 한 변의 길이의 비율은 정수비로 표현할 수 없다는 것을 발견했습니다. 따라서 그 비율을 정수로 이루어진 비인 유리수로 표현할 수 없습니다. 그는 이것을 '설명 불가'라고 칭했습니다. 무리수를 위협으로 생각했기 때문에 무리수의 패턴을 찾으려고 시도했습니다. 하지만 결국 패턴을 찾아내지 못했습니다. → 고정밀 계산이 필요한 또 하나의 이유가 됩니다. 👀 무리수에 숨겨진 특정한 패턴이 있을까요? ⁉️ 카탈란 수 : 올바른 괄호 구조 문자열로 이루어진 집합 P는 아래와 같이 귀납적으로 정의합니다. λ ∈ P (λ: 빈 문자열) 만약 α, β ∈ P이면, (α)β..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 개방 주소법 ⁉️ 충돌을 대처하는 또 다른 방법 체이닝 없이 모든 항목이 테이블에 저장됩니다. 한 슬롯당 하나의 항목입니다. ⇒ m(해시 테이블의 슬롯 크기) ≥ n(항목 수) ⁉️ 조사 해시 함수는 키 삽입/탐색/삭제를 위한 키의 슬롯의 탐색 순서를 정합니다. 해시 함수는 하나의 슬롯만 보는 게 아닙니다. 소학적으로 표현하면 다음과 같습니다.(모든 k ∈ μ인 특성을 가진 해시 함수 h를 만들고 싶을 때) 는 0, 1, … , m − 1의 순열입니다. 즉, i를 하나씩 늘려가며 h(k, i)를 다 돌면, 표에 있는 모든 슬롯을 돌게 됩니다. ⁉️ Insert(k, v) : 빈 슬롯을 찾을 때까지 계속 ..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 테이블 더블링 ⁉️ 해시 테이블의 크기는 얼마나 커야 하나? 해시 테이블(지난 강의 참조)의 경우 m과 n이 비슷할 경우가 가장 좋지만 n을 알 수가 없습니다. m이 너무 작으면 느리고 m이 너무 크면 낭비가 됩니다. 그리고 항상 m = Θ(n) 이길 원합니다. ⁉️ 발상 : 작은 상수로 시작해 필요에 따라 늘리거나 줄입니다. ⁉️ 다시 해싱하기 : 해시 테이블을 늘리거나 줄이기 위해서는 해시 함수의 (m, r)도 바뀌어야 합니다. ⭐ m → m'로 테이블 사이즈를 변경할 경우 m' 사이즈 테이블을 생성 h'라는 새로운 해시 함수 생성 다시 해싱하기 for 항목 in 기존 테이블: 새로운테이블.inser..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 딕셔너리 : 추상 자료형(ADT)으로 일반적으로 딕셔너리는 각각의 항목에 키가 존재하는 집합이라 합니다. 균형 이진 탐색 트리는 연산 하나당 O(lg n) 시간이 소요되었는데 딕셔너리는 연산 하나 당 O(1) 시간이 목표입니다. insert(item): 집합에 항목 추가(존재하는 키는 덮어씀) delete(item): 집합에서 항목 제거 search(key): 존재할 경우 키와 항목 반환(존재하지 않을 경우 key error 발생) ⁉️ 파이썬의 딕셔너리 : 항목은 (키, 값) 쌍으로 이루어져 있습니다. 파이썬 집합은 항목이 곧 키가 되는 진짜 dict(사전)에 가깝습니다.(값이 없음을 의미합니다.) ⁉..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 비교 모델 : 비교 모델의 아이디어는 비교를 할 때 어떤 연산을 사용할지 제한하는 것입니다. 모든 입력 항목은 블랙박스입니다.(ADTs) → 블랙박스 : 정확히 무엇인지 모른다는 것을 의미 유일하게 가능한 연산은 비교입니다.(, ≥, =) 시간 비용은 단순히 비교한 횟수로 정의합니다. ✔ 의사 결정 나무(Decision tree) : 어떠한 비교 알고리즘에서도 비교할 수 있는 모든 경우의 수와 비교 결과 및 최종 결론으로 이루어진 트리로 표현할 수 있습니다. 특정한 값 n(문제의 크기)부터 시작하는 것입니다. 의사 결정 나무 알고리즘 내부 노드 이진 결정(비교 모델만 다룸) 단말 노드 찾는 답에 해당 루..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 복습: 이진 탐색 트리(BST) 루트가 있는 이진 트리 각 노드는 다음을 가짐 : [ 키, 왼쪽 포인터, 오른쪽 포인터, 부모 포인터 ] 노드의 높이 = 단말 노드까지의 가장 긴 하향 경로의 길이 ⭐ 노드의 높이는 자식 노드들 높이 중 가장 큰 값에 1을 더함 ⭐ 자식 노드가 없는 부모 노드는 자식 노드 부분 높이를 -1로 설정 각 노드는 자신의 높이를 저장((높이 대신 높이의 차를 저장할 수도 있음) ✔ 균형을 이루는 것의 중요성 이진 탐색 트리는 삽입, 삭제, 최솟값, 최댓값, 다음으로 큰 값 찾기, 다음으로 작은 값 찾기 등을 O(h) 안에 실행할 수 있습니다. 이때 h=트리의 높이(=루트의 높이)..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 활주로 예약 시스템 활주로가 매우 혼잡하고 단 하나뿐인 공항(보스턴 6→1) 향후 착륙을 위한 "예약" 비행기가 착륙하면 대기 중인 사건 집합에서 제거하기 각각의 착륙 요청에는 "요청 예약 시간" t가 명시되어 있음 t로부터 k분 전이나 k분 후에 다른 착륙 예약이 없다면, t를 집합에 추가함. k값은 변할 수 있음 → 그 외의 경우는 에러로 보고, 예약을 잡지 않음 ⁉️ 예시 R은 예약된 착륙 시간을 나타냄: R = (41, 46, 49, 56)과 k=3 착륙 시간 요청 : 44는 허용되지 않음(46∈R) 53 허용 20 허용되지 않음(이미 지난 시간) |R| = n 목표 : 본 시스템을 O(log n..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 우선순위 큐 요소들 집합 S를 구현하는 자료구조입니다. 각 요소들은 key와 관련이 있고 다음 작업들을 지원합니다. insert(S, x) : 요소 x를 집합 S에 삽입 max(S) : 최대 key인 S의 요소를 반환 extract_max(S) : 최대 key인 S의 요소를 반환하고 집합 S에서 x 제거 increase_key(S, x, k) : 요소 x의 key를 새로운 값 k로 증가(k가 현재 값만큼 크다고 가정) ✔ 힙 우선순위 큐의 구현 가능 완전 이진 트리로 시각화된 배열 최대 힙 특성은 노드의 key가 자식 값들의 key보다 크거나 같음(최소 힙도 마찬가지로 동일하게 정의) ⁉️ 트리로서의 힙..

BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다. ✔ 정렬 ⁉️ 정렬이란? 배열의 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 것입니다. ⁉️ 왜 정렬을 해야 할까? 대표적인 응용 사례 : 전화번호부 정리, 검색, mp3 파일 관리, 스프레드시트 등 정렬되면 쉬워지는 문제들 : 중간값 또는 가장 가까운 쌍 찾기, 이진탐색/통계적 이상치 확인 생소한 응용 사례 : 데이터 압축(정렬로 중복된 부분 검출), 컴퓨터 그래픽(앞에서 뒤로 화면 렌더링) ⁉️ 삽입 정렬 👀 삽입 정렬이란? 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입함으로써 정렬하는 방법입니다. ⏱ 시간 복잡도 : Θ(n^2) 👀 ..