BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 정의

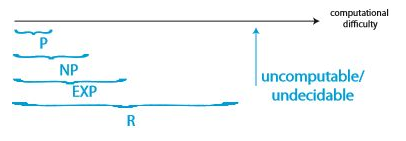
P
: 다항 시간에 풀 수 있는 모든 문제들의 집합
예시) 음수 가중치 사이클 탐지 ∈ P
EXP
: 지수 시간에 풀 수 있는 모든 문제들의 집합.
예시) n×n 체스 ∈ EXP 그러나 ∈/(속하지 않음) P → n×n 체스 주어진 보드 배열에서 누가 이기는가?
R
: 유한 시간에 풀 수 있는 모든 문제들의 집합
예시) 테트리스 ∈ EXP 그러나 ∈ P 인지는 모름 → 주어진 보드와 조각들에서 살아남기
정지 문제
: 컴퓨터 프로그램이 주어졌을 때, 그것이 한 번이라도 정지하는가?
- 계산 불가능 (∈ / R):이것을 푸는 알고리즘은 없다 (모든 입력값에 대해 유한 시간에 맞게 푸는 것)
- 결정 문제: 답은 예 또는 아니오
대부분의 결정 문제들은 계산 불가능
- 프로그램 ≈ 이진 문자열 ≈ 음수가 아닌 정수 ∈ N
- 결정 문제 = 이진 문자열 (≈ 음수가 아닌 정수)에서 {예 (1), 아니오 (0)}로 변환하는 함수
- ≈ 비트의 유한한 나열 ≈ 실수 ∈R |N| << |R|:고유한 음수가 아닌 정수를 실수에 할당할 수 없음 (R 셀 수 없음)
⇒ 모든 문제에 대한 프로그램이 없음 - 모든 프로그램은 한 개의 문제를 푼다
⇒ 대부분의 문제들은 풀 수 없음
NP
: "행운" 알고리즘을 통해 다항 시간에 해결 가능한 결정 문제의 집합
→ NP는 다항 시간에 “확인”될 수 있는 해답이 있는 결정 문제들 집합. 답 = YES이면, “증명” 가능 & 다항 시간 알고리즘으로 확인 가능
- 비결정적 모델: 알고리즘은 추측을 하고 예 또는 아니오를 도출
- 만약 가능하다면 추측이 예를 도출하는 것이 보장됨 (불가능하다면 아니오)
예시) 테트리스 ∈ NP
- 비결정적 알고리즘: 각 움직임들을 추측하자. 살아남았는가?
- 예에 대한 증명: 움직임들의 리스트 (테트리스의 규칙은 쉬움)
P ≠ NP
큰 추측 ($1,000,000 가치)
≈ 운을 설계할 수 없습니다
≈ 해답을 만드는 것은 그것을 확인하는 것보다 어렵습니다
✔ 난해성과 완전성
주장
: 만약 P ≠ NP이면, 테트리스 ∈ NP - P입니다.
이유
: 테트리스는 NP-난해 = 모든 문제 “만큼 어렵다” ∈ NP. NP-완전 = NP ∩ NP-난해

✔ 리덕션
처음부터 해결하는 대신 문제를 이미 해결법을 아는 문제로 바꿉니다.
- 가장 보편적인 알고리즘 디자인 기술
- 비가중치 최소 경로 → 가중치 (가중치 = 1로 둡니다)
- 최소 곱 경로 → 최단 경로 (로그를 취합니다)
- 최장 경로 → 최단 경로 (가중치를 음수로)
- 최단 순서 순회 → 최단 경로 (그래프의 k개의 복사본)
- 최소 가격 구멍 난 탱크 경로 → 최단 경로 (그래프 리덕션)
위의 모든 문제들은 원-콜 리덕션
: 문제 A → 문제 B → 해답 B → 해답 A
멀티콜 리덕션
: B를 제한 없이 호출해서 A를 해결합니다. 이런 의미에서, 모든 알고리즘은 문제를 축소시킵니다 → 계산 모델
NP-완전 문제들은 다항 시간 리덕션을 사용해서 서로 간에 축소가 가능합니다 (같은 난이도). 따라서 NP-난해성을 증명하는 데에 리덕션을 사용할 수 있습니다.
예) 3-분할 → 테트리스
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [코딩 인터뷰]자료구조 - 배열과 문자열 (0) | 2022.11.29 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘 : 병렬 프로세서 구조 & 알고리즘 (0) | 2022.11.22 |
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 4 (0) | 2022.11.17 |
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 3 (0) | 2022.11.16 |
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 2 (2) | 2022.11.15 |