BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 복습
⁉️ 동적 프로그래밍의 5단계
- 하위 문제 정의하기 ⇒ 하위 문제의 개수 세기
- (해법의 일부분을) 추측하기 ⇒ 선택지의 개수 세기
- 하위 문제의 풀이 연관짓기 ⇒ 하위 문제당 시간 계산
- 재귀+기억 또는 DP 테이블을 상향식으로 만들기 ⇒ 시간 = 하위 문제당 시간·하위 문제의 개수
하위 문제가 비순환적인지/위상학적 순서인지 확인하기 - 원래 문제 풀이 ⇒ 추가 시간 필요
: 하위 문제의 풀이 또는 하위 문제들로 조합하여 풀기
⁉️ 텍스트 정렬, 블랙잭은 시퀀스와 관련있습니다.(단어, 카드의 시퀀스)
⁉️ 문자열/시퀀스 x에 대해 유용한 문제들
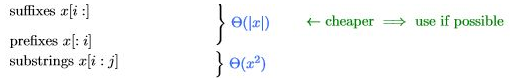
✔ 괄호 묶기
: A[0] · A[1]···A[n − 1]를 계산하는 최적의 방법입니다.
예시) 행렬의 곱셈

1. 추측 : 가장 바깥의 곱셈 혹은 마지막 곱셈
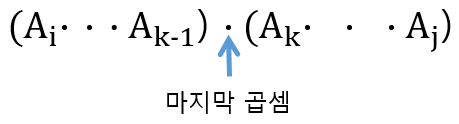
⇒ 선택의 수 = O(j-i+1) = O(n)
2. 하위 문제 : 부분 문자열 A[i : j]의 비용
⇒ 하위 문제의 개수 = Θ(n^2)
3. 반복
- DP[i, j] = min(DP[i, k] + DP[k, j]+ (A[i]···A[k−1])과 (A[k]···A[j−1])를 곱하는 데 필요한 비용 (for k in range(i + 1, j))
- DP[i, i+1] = 0
⇒ 하위 문제당 비용 = O(j - i) = O(n)
4. 위상학적 순서 : 부분 문자열 크기의 오름차순
⇒ 총 시간 = Θ(n^3)
5. 원래 문제 : DP[0, n]
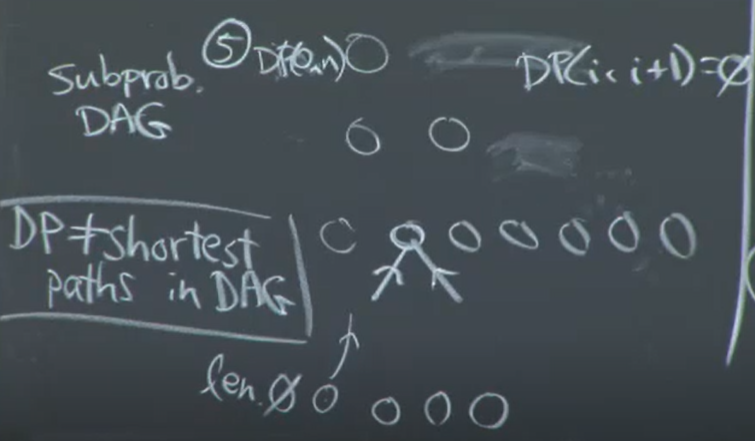
👀 이 DP는 DAG의 최단 경로가 아닙니다. 두 개의 노드에 의존하기 때문에 경로가 아닙니다.
✔ 편집 거리
DNA 비교, 차이, CSV/SVN/..., 철자 확인(오타), 표절 탐지 등. 주어진 두 개의 문자열 x&y에 대해 x를 y로 바꿀 때 가장 값싼 편집(c 삽입, c 삭제, c → c'로 교체)의 시퀀스는 무엇인가요?
- 편집의 비용은 오직 문자 c, c'에 의존합니다.
예를 들어 DNA에서, C → G는 흔한 변형이므로 ⇒ 비용이 저렴합니다. - 시퀀스의 비용 = 편집 비용의 합
만약 삽입/삭제의 비용이 1, 교체의 비용이 0(c=c') 또는 무한대(c!=c')이라면 이 문제는 최장 길이 공통부분 시퀀스를 찾는 문제입니다.
Note : 부분 시퀀스는 문자열 안에서 연속된 것일 필요는 없습니다. - 예시)
H I E R O G L Y P H O L O G Y vs. M I C H A E L A N G E L O ⇒ HELLO
⁉️ 여러 개의 문자열/시퀀스에 대한 문제
- suffix/prefix 부분 문자열 하위 문제를 통합
- 상태의 크기들을 곱함
- O(1) 문자열에 대해 여전히 다항식 형태
⁉️ 편집 거리 DP
1. 하위 문제 : DP(i, j) = 편집 거리(x[i :],y[j :]) for 0 ≤ i < |x|, 0 ≤ j < |y|
⇒ Θ(|x|·|y|) 만큼의 하위 문제가 존재
2. 추측 : x를 y로 바꾸기 위해

- x[i]를 삭제
- y[j]를 삽입
- x[i]를 y[j]로 교체
3. 반복 : DP(i, j) = 아래 중 최댓값
- x[i]를 삭제하는 비용 + DP(i+1, j) if i < |x|
- y[j]를 삽입하는 비용 + DP(i, j+1) if j < |y|
- x[i] 를 y[j]로 교체하는 비용 + DP(i + 1, j + 1) if i < |x|&j < |y|
기본 단계 : DP(|x|,|y|) = 0
⇒ 하위 문제당 Θ(1)만큼의 시간이 필요합니다.
4. 위상학적 순서 : DAG를 2차원 표로 나타낼 수 있습니다.

- ↑(밑에서 위로) 혹은 ←(오른쪽에서 왼쪽으로)
- 마지막 2개의 행/열만 유지하고 있으면 됩니다. ⇒ 선형 크기 공간
5. 원래 문제 : DP(0, 0)
⇒ 총 시간 = Θ(|x|·|y|)
✔ 배낭 문제
: 크기 S의 가방에 짐을 넣고 싶을 때 물건 i는 정수 형태의 크기 si와 실제 가치 vi를 가지고 있습니다. 가치를 최대로 하면서 총 크기 ≤ S를 만족하도록, 가져갈 수 있는 물건의 목록 만드는 것입니다.
⁉️ 풀이
1. 하위 문제 : suffix i의 가치, 주어진 크기 X의 가방
⇒ 하위 문제의 개수 = O(nS)
2. 추측 : 물건 i를 가져갈지 말지 선택(2가지 선택 사항)
3. 반복
- DP(i, X) = max(DP(i+1, X), vi + DP(i+1, X−si] if si ≤ X)
- DP(n, X) = 0
⇒ 하위 문제당 필요한 시간 = O(1)
4. 위상학적 순서
⇒ 총 시간 = Θ(nS)
* 다항 시간이 아닌 유사 다항 시간입니다.
5. 원래 문제 : DP[0, S]
👀 가져갈 물건의 집합의 모든 경우를 효율적이라고 고려하지만 실제로 빠른지는 의문입니다.
⁉️ 다항 시간
: 입력값 크기에 대해 다항식으로 표현 가능합니다. 만약 위의 총 시간 S가 한 워드에 들어간다면 Θ(n)이라 할 수 있습니다. 일반적으로 O(nlgS)에 대한 S는 lgS에 대해 지수적이기에 다항식이라 할 수 없습니다.
⁉️ 유사 다항 시간
: 입력값의 크기에 대해 다항식과 입력으로 받는 수자들로 표현 가능합니다. (예시: S, s ’s, ’s). Θ(nS)는 유사 다항 시간입니다.
⭐ 기억할 것
다항 - 좋음 유사 다항 - 보통 지수 - 나쁨
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘 : 계산 복잡도 (0) | 2022.11.21 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 4 (0) | 2022.11.17 |
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 2 (2) | 2022.11.15 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 동적 프로그래밍 1 : 메모이제이션, 피보나치 수, 최단 경로, 추측 (0) | 2022.11.14 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 4 : 다익스트라 가속화 (1) | 2022.11.11 |