BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 딕셔너리
: 추상 자료형(ADT)으로 일반적으로 딕셔너리는 각각의 항목에 키가 존재하는 집합이라 합니다. 균형 이진 탐색 트리는 연산 하나당 O(lg n) 시간이 소요되었는데 딕셔너리는 연산 하나 당 O(1) 시간이 목표입니다.
- insert(item): 집합에 항목 추가(존재하는 키는 덮어씀)
- delete(item): 집합에서 항목 제거
- search(key): 존재할 경우 키와 항목 반환(존재하지 않을 경우 key error 발생)
⁉️ 파이썬의 딕셔너리
: 항목은 (키, 값) 쌍으로 이루어져 있습니다. 파이썬 집합은 항목이 곧 키가 되는 진짜 dict(사전)에 가깝습니다.(값이 없음을 의미합니다.)

⁉️ 동기
: 파이썬에서 딕셔너리가 만들어진 이유는 파이썬에서 필요하기 때문입니다.
- 문서 거리 문제(단어 세기 & 내적) 사용
- 현대 프로그래밍 언어에 다 내장(Python, Perl, Ruby, JavaScript, Java, C++, C#...)
- 데이터베이스 구현
- 컴파일러 & 인터프리터: 이름 → 변수
- 네트워크 라우터: IP 주소 → 랜선
- 네트워크 서버: 포트 번호 → 소켓/앱
- 가상 메모리: 가상 주소 → 물리적 주소
그 외에도 간접적으로 쓰는 경우:
- 부분 문자열 탐색(grep, Google)
- 염기 공통성(DNA)
- 파일 또는 디렉터리 동기화
- 암호학: 파일 변환 & 식별
✔ 딕셔너리 문제를 어떻게 풀까요?
간단한 접근법으로 직접 접근 테이블을 사용하는 것입니다. 인덱스가 키가 되며, 항목은 배열에 저장되어야 합니다.

⁉️ 문제점
- 키가 정수가 아닐 수 있습니다.
- 공간 낭비가 심합니다.
⁉️ 해결법
1번에 대한 해결법: 키를 정수로 "프리 해시(prehash)"
- 프리 해시 함수는 어떤 키든 간에 음이 아닌 정수로 대응시켜 줍니다.
- 이론적으로 키는 유한하고 불연속적입니다. 그래서 키의 집합을 셀 수 있습니다.
- 파이썬은 해시(사실 "프리 해시"가 정확한 표현) 객체는 숫자, 문자열, 튜플 등 또는 __hash__가 구현된 객체가 될 수 있습니다.(기본값=id=메모리 주소)
- 이론적으로 hash(x)=hash(y)일 때는 x=y일 때만 가능하지만 파이썬은 실용성을 위해 경험적인 방법을 일부 적용했습니다.
(예: hash('\0B')=64=hash(''\0\0C')) - 테이블에서 객체의 키는 바뀌어서는 안 됩니다. 바뀌면 더 이상 찾을 수 없습니다.
- 리스트와 같은 가변 객체는 안됩니다.
2번에 대한 해결법: 해싱
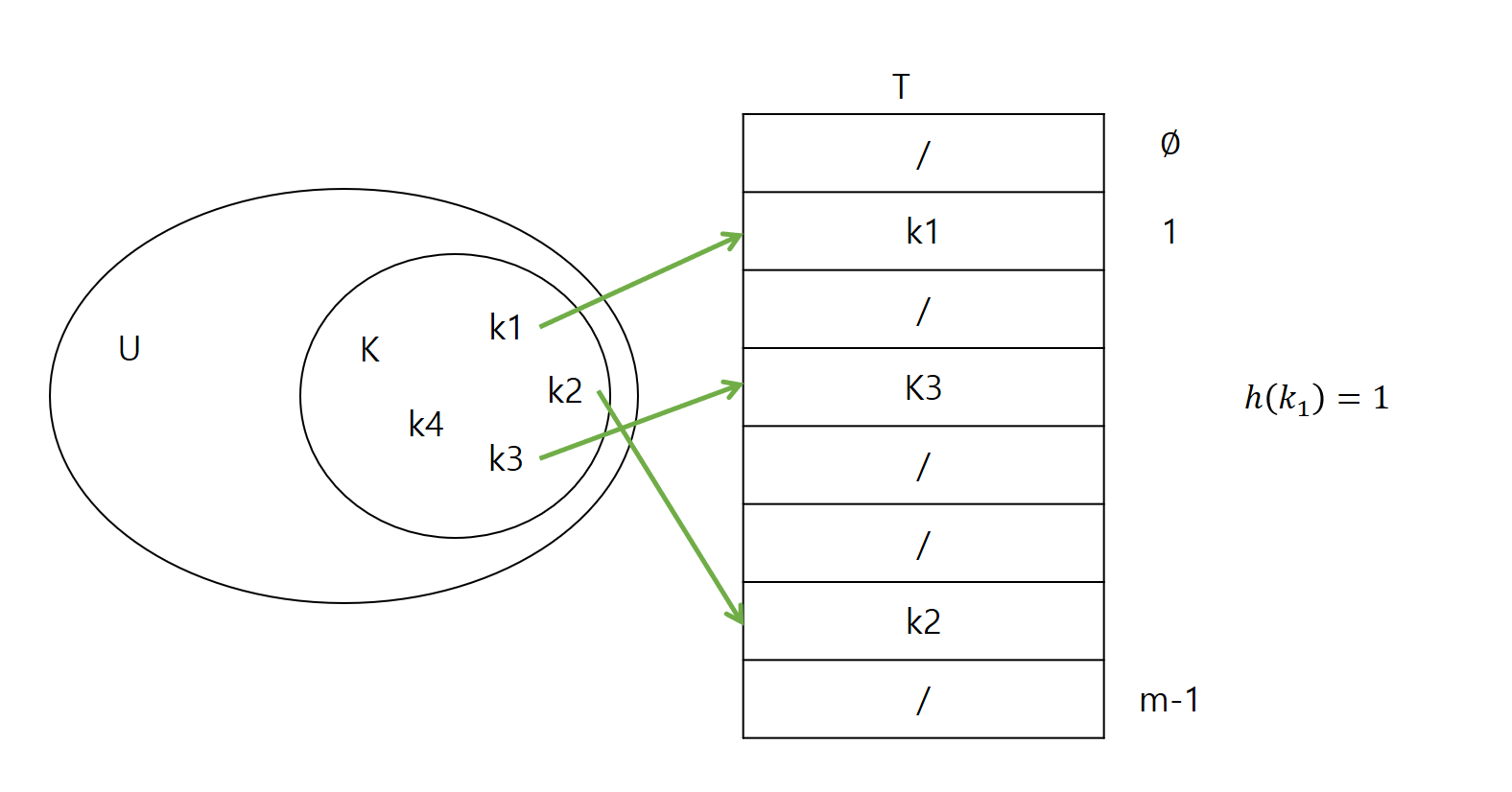
- 모든 키(예를 들면 정수)가 있는 전체집합 U를 합리적인 크기 m인 테이블로 줄이는 것입니다.
- 그다음 m이 n과 비슷한 값을 갖도록 합니다.
m ≈ n(딕셔너리에 저장된 키의 개수) → 테이블의 크기는 딕셔너리에 있는 키의 개수에 비례하게 됩니다.
해시 함수 h:U →{0,1,..., m−1} - 키 충돌이 일어날 수 있습니다. 이러한 충돌에는 2가지 방법(체이닝, 개방 주소법)이 존재합니다.
키 충돌: 여러 개의 키가 해시 테이블의 같은 슬롯에 대응되는 것입니다.
⁉️ 체이닝
: 해시 테이블에 충돌 원소가 생긴 슬롯을 링크드 리스트로 연결합니다.

- 탐색 시 리스트 전체인 T[h(key)]를 훑어야 합니다.
- 최악의 경우: 모든 n개의 키가 같은 슬롯에 있는 경우 ⇒ 연산 당 Θ(n)입니다.
✔ 단일 균일 해싱
⁉️ 가정
모든 키는 테이블의 아무 슬롯에나 해시될 가능성을 동등하게 가지고 있습니다. 각 키의 해시는 독립적으로 다른 키가 해시되었는지와 상관없습니다.
- let n = 테이블에 저장된 키의 개수
- m = 테이블의 슬롯 개수
- 적재율 α = n/m = 슬롯 당 예상되는 키의 개수 = 체인의 예상되는 길이
⁉️ 성능
탐색의 예상되는 실행 시간이 Θ(1+α)라는 의미 합니다. 1은 해시 함수를 적용하고 슬롯에 임의 접근하는 것을 의미하는 반면 α는 리스트를 탐색하는 것을 의미합니다. α = O(1)이면 O(1)이 됩니다. (즉, m = Ω(n))
⁉️ 해시 함수
위와 같은 성능을 달성하는 방법으로 3가지가 있습니다.
- 분할 방법(나머지 연산법) : h(k) = k mod m
m이 2의 제곱이나 10의 제곱에 가까이 있지 않은 소수일 경우 실용적입니다. - 곱셈 방법 : h(k) = [a(a(a·k) mod 2 w] ≫ (w-r)
a는 임의 값, k는 w 비트 그리고 m=2^r입니다. a가 홀수 & 2^(w-1) < a< 2^w & a가 2^(w-1) 또는 2^w에 너무 가깝지 않아야 이 방법이 실용적입니다. - 유니버설 해싱 : h(k) = [(ak+b) mod p] mod m
a 와 b는 임의 값 ∈{0,1,... p−1}, 그리고 p는 큰 소수 (> |U|)입니다. 최악의 경우에는 키가 k1 ≠ k2입니다. (h의 선택 a, b에 의해)

'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 3: 개방 주소법 (0) | 2022.10.27 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 2 (0) | 2022.10.25 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 선형 시간 정렬(정수 정렬) (0) | 2022.10.21 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 균형 이진 탐색 트리 (0) | 2022.10.20 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 일정 예약과 이진 탐색 트리 (0) | 2022.10.19 |