BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 개방 주소법
⁉️ 충돌을 대처하는 또 다른 방법

- 체이닝 없이 모든 항목이 테이블에 저장됩니다.
- 한 슬롯당 하나의 항목입니다. ⇒ m(해시 테이블의 슬롯 크기) ≥ n(항목 수)
⁉️ 조사
해시 함수는 키 삽입/탐색/삭제를 위한 키의 슬롯의 탐색 순서를 정합니다. 해시 함수는 하나의 슬롯만 보는 게 아닙니다. 소학적으로 표현하면 다음과 같습니다.(모든 k ∈ μ인 특성을 가진 해시 함수 h를 만들고 싶을 때)

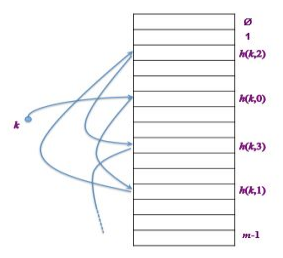
<h(k, 0), h(k, 1) ... h(k, m-1)>는 0, 1, … , m − 1의 순열입니다. 즉, i를 하나씩 늘려가며 h(k, i)를 다 돌면, 표에 있는 모든 슬롯을 돌게 됩니다.
⁉️ Insert(k, v)
: 빈 슬롯을 찾을 때까지 계속 조사하고 항목을 그 슬롯에 넣습니다.
for i in xrange(m):
if T[h(k, i)] is None: # empty slot
T[h(k, i)] = (k, v) # store item
return
raise 'full'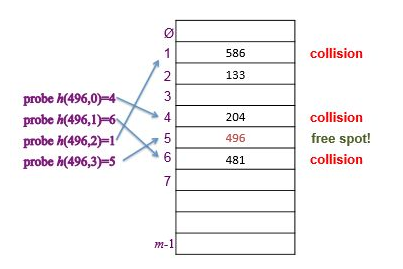
⁉️ Search(k)
: 조사를 통해 확인한 슬롯에 있는 키가 k가 아니면 k를 찾을 때까지 또는 빈 슬롯을 찾을 때까지 계속 조사합니다. 각각 성공이나 실패를 반환합니다.
for i in xrange(m):
if T[h(k, i)] is None: # empty slot?
return None # end of "chain"
elif T[h(k, i)][0] == k # matching key
return T[h(k, i)] # return item
return None # exhausted table
⁉️ 항목 삭제
항목을 찾아서 그 슬롯에서 바로 지우면 안 됩니다. (예시. T[h(k, i)] = None)(예시:delete(586) ⇒ search(496) 이 실패합니다.) 그 항목을 새로운 표시 "DeleteMe"로 바꿉니다 그리고 데이터 삽입시에는 None으로 여기고, 탐색에는 None으로 여기지 않습니다.
✔ 조사 기법
⁉️ 선형 조사
h(k, i) = (h'(k) + i) mod m
여기서 h'(k)는 평범한 해시 함수입니다. 이 조사 집단의 잘못된 점은 군집화 집단입니다. 대부분의 적재율에서 해시 테이블에 선형 조사를 사용하면 평균 상수 시간 성질을 잃는다는 것을 알 수 있습니다.
- 군집화 집단
: 값이 차 있는 연속된 슬롯의 무리는 계속해서 커지고 커질 확률이 점점 높아집니다.
→ 0.01<α< 0.99 이면, 군집의 크기가 Θ(log n)입니다.

⁉️ 이중 해싱
h(k, i) = (h1(k) + i · h2(k)) mod m
여기서 h1(k)와 h2(k)는 두 개의 평범한 해시 함수입니다. 모든 k에 대해 h2(k)와 m이 서로소이면 모든 슬롯을 확인할 수 있다.
h1(k) + i · h2(k) mod m = h1(k) + j + h2(k) mod m ⇒ m divides (i - j)
예시로 한 가지 살펴보면 m = 2^r이면 h2(k)를 항상 홀수면됩니다.
✔ 균일한 해싱, 분석
⁉️ 균일한 해싱 가정
각 키가 가지는 탐색 순서는 무작위의 순열인데 그 m!의 순열 중에 특정 순열이 될 확률은 모두 같습니다. 실제로는 매우 어렵지만 이중 해싱을 사용하면 비슷하게 할 수 있습니다.
⁉️ 분석
개방 주소법을 써서 n개의 항목을 m 크기의 표에 삽입했다고 가정합니다. 균일한 해싱을 가정하면, 다음 연산의 기대 비용은 1/(1-α) 이하입니다. 여기서 α=n/m(<1)입니다.
⁉️ 증명
: k라는 키를 가진 항목을 삽입하고 싶다고 가정합니다. 그리고 그 항목이 표에 없다면
- 첫 조사가 성공할 확률은 (m-n)/m=:p입니다.
(이미 찬 슬롯 수는 n, 총 슬롯 수는 m, 첫 조사는 균일한 무작위성을 가집니다.) - 첫 조사가 실패하면 두 번째 조사가 성공할 확률은 (m-n)/(m-1) ≥(m-n)/m = p입니다.
(이미 찬 슬롯 중 두 개는 어딨는지 알고, m-n개의 빈 슬롯이 있습니다. 두 번째 조사는 남은 m-2개의 슬롯에서 균일한 무작위성을 가집니다.)
⇒ 모든 시도가 적어도 p 이상의 성공 확률을 가집니다.
⁉️ 성공까지 기대 시도 횟수는?

데이터 탐색과 삭제는 O(1/(1 − α)) 만큼 걸립니다. 이미 있는 항목을 삽입할 때도 같습니다.
⁉️ 개방 주소법 vs 체이닝
개방주소법
: 더 나은 캐시 성능을 가졌습니다. (더 나은 메모리 사용, 포인터를 쓸 필요 없음)
체이닝
: 적재율(적재율이 70%을 넘으면 저하된다. 적재율이 1을 넘으면 안 된다.)과 해시 함수(개방 주소법은 군집화를 막아야 한다.)에 제한이 적습니다.
✔ 암호학적 해싱
암호학적 해시 함수는 임의의 데이터를 받아 정해진 크기의 문자 열과 (암호화된) 해시 값을 반환합니다. 고의 또는 실수로 데이터가 바뀌면 해시 값도 바뀝니다. 암호화된 데이터는 대부분 메시지라고 불리는데 해시 값이 메시지 다이제스트 또는 다이제스트라고도 불립니다.
⁉️ 암호 해독 해시 함수의 특성
- 일방성(One-Way, OW)
: y ∈ {0, 1} 이런 y가 주어졌을 때, d h(x)=y의 x를 찾는 것은 불가능합니다. 이 말인즉, 무작위의 d-bit 벡터를 골랐을 때, 그 벡터를 해시 값으로 가지는 입력 값을 찾지 못한다는 것입니다. - 충돌 저항(Collision-resistance, CR)
: h(x)=h(x′)을 만족시키는 두 개의 다른 x와 x′은 존재하지 않습니다. 이렇게 두 가지 입력 값이 같은 해시 값을 가지는 것을 충돌이라 부릅니다. - 목표 충돌 저항(Target collision-resistance, TCR)
: x가 주어진 상태에서 x와 x’은 다르고 h(x)=h(x’)인 x’를 찾는 것은 거의 불가능합니다
TCR은 CR보다 약한 조건이기 때문에 어떤 해시 함수가 CR을 만족시키면 TCR도 같이 만족시킵니다. 하지만 OW와 CR/TCR은 관계가 없습니다.
👀 아래의 부분은 강의에는 없는 제공된 자료물 내용입니다.
⁉️ 응용
- 비밀번호 저장소
: 컴퓨터에 PW가 아닌 h(PW)를 저장합니다. 사용자가 PW′를 입력하면 h(PW′)를 계산해 저장되어 있는 h(PW)와 비교합니다. 해시 함수는 OW를 만족해야 합니다. 상대방이 PW나 PW′를 모르기 때문에 TCR이나 CR이 필요 없습니다. 많은 비밀번호가 같은 해시 값을 가지면 문제지만, 약간의 충돌은 보안에 큰 영향을 끼치지 않습니다. - 파일 변경 탐지기
: F라는 각 파일마다 h(F)를 안전하게 저장합니다. F가 바뀌었는지는 h(F)를 다시 계산해보면 알 수 있습니다. 해시 함수가 TCR을 만족해야 합니다. 상대방이 h(F)를 바꾸지 않고 F를 바꿀 수 있으면 안 됩니다. - 디지털 서명
: 공개된 키 암호 해독에서, 앨리스가 PKA라는 공개된 키와 SKA라는 개인 키가 있다고 할 때 앨리스가 개인 키를 써서 σ = sign(SKA, M)을 만들고, 메시지 M에 서명을 할 수 있습니다. 앨리스의 공개된 키 PKA를 아는 사람은 앨리스의 서명의 진위여부를 verify(M, σ, PKA)가 true인지를 통해 알 수 있습니다. 상대방은 서명을 위조하려 할 때 큰 M의 경우, h(M)을 서명하는 게 M에 서명하는 것보다 쉽습니다. 즉, σ = sign(SKA, h(M)). 그러면 CR을 만족해야 합니다. h(x) = h(x’)이면, 상대방이 A에게 x를 서명하라 하고 앨리스가 x0에 서명했다고 말할 수 없어야 합니다.
⁉️ 구현
OW, CR 그리고 TCR을 만족시킨다고 주장된 해시 함수가 많습니다. 하지만 몇 개는 완전하지 못합니다.(예를 들어 MD-5는 CR이 아니라고 밝혀졌습니다.) NIST에 의해 인증된 안전한 해시 알고리즘인 SHA-3을 결정짓기 위한 경쟁도 계속해서 진행되고 있습니다. 암호 해독 해시 함수는 해시 표에서 쓰이는 함수들 보다 훨씬 복잡합니다. 암호 해독 해시는 보통 해시 함수를 의사 난수 순열을 여러 번 덧붙여서 하는 거라고 생각해도 됩니다.
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수2 (0) | 2022.11.01 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수1 (0) | 2022.10.31 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 2 (0) | 2022.10.25 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 1 (0) | 2022.10.24 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 선형 시간 정렬(정수 정렬) (0) | 2022.10.21 |