BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 테이블 더블링
⁉️ 해시 테이블의 크기는 얼마나 커야 하나?
해시 테이블(지난 강의 참조)의 경우 m과 n이 비슷할 경우가 가장 좋지만 n을 알 수가 없습니다. m이 너무 작으면 느리고 m이 너무 크면 낭비가 됩니다. 그리고 항상 m = Θ(n) 이길 원합니다.
⁉️ 발상
: 작은 상수로 시작해 필요에 따라 늘리거나 줄입니다.
⁉️ 다시 해싱하기
: 해시 테이블을 늘리거나 줄이기 위해서는 해시 함수의 (m, r)도 바뀌어야 합니다.
⭐ m → m'로 테이블 사이즈를 변경할 경우
- m' 사이즈 테이블을 생성
- h'라는 새로운 해시 함수 생성
- 다시 해싱하기
for 항목 in 기존 테이블:
새로운테이블.insert(항목)
⁉️ 늘리는데 소요되는 시간은?
- m' = m+1이면?
→ 매번 새롭게 늘려야 합니다.
→ n번의 삽입이 Θ(1 + 2 +···+ n) = Θ(n^2)만큼 걸립니다. - m' = 2m이면? ⇒ 테이블 더블링
→ 2^i번마다 새롭게 해시 테이블을 만들어줍니다.
→ n번의 삽입이 Θ(1 + 2 + 4 + 8 +···+ n) = Θ(n)만큼 걸립니다. n은 바로 다음 2의 제곱일 때 몇몇의 삽입은 선형시간이 걸리지만, 평균적으로는 Θ(1)만큼 걸립니다.
👀 분할상환으로 이동했다가 돌아오기
⁉️ 데이터 삭제
1. 만약 m = n/2이라면 → m/a
⇒ 이 방법은 느립니다. Θ(n) 시간을 가지게 됩니다.
2. 만약 m = n/4이라면 → m/2
⇒ Θ(1) 분할상환 시간이 걸립니다. 그리고 해시 테이블은 선형 크기를 갖게 됩니다.(n ≤ m ≤ 4n)
⁉️ 크기 조절이 가능한 배열
- 같은 기법이 파이썬의 "리스트"(배열)에도 쓰입니다.
- ⇒list.append와 list.pop은 Θ(1) 분할상환 시간이 걸립니다.

⁉️ 문자열 매칭
두 개의 문자열 s와 t가 주어졌을 때, s가 t의 부분 문자열입니까?(그리고 그렇다면, 어디에 몇 개나 있습니까?)
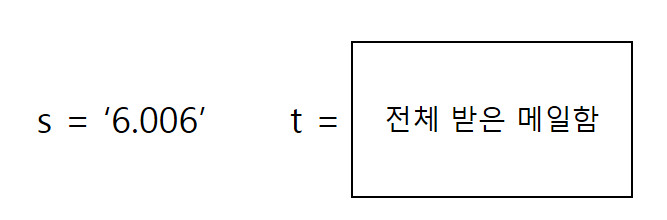
⭐ 간단한 알고리즘
any(s==t[i:i+len(s)] for i in range(len(t)-len(s)))
: Θ(|s|) 시간이 각 부분 문자열을 비교할 때 걸립니다.
⇒ 총 Θ(|s|·(|t|-|s|))= O(|s|·|t|)이 걸립니다. 이 방법은 좋은 방법이 아니기 때문에 해싱을 이용한 다른 방법이 필요합니다.
👀 Karp-Rabin 알고리즘으로 이동
✔ 분할상환
데이터 구조에서 자주 쓰는 기법입니다. $1500 월세를 하루에 $50씩 나눠내는 것과 비슷합니다.
- k번의 연산 시간 ≤ k·T(n)이면, 연산이 분할상환 실행시간 T(n)이 듭니다.
- "분할상환 T(n)"은 대략 "평균적으로" T(n)을 의미하고, 모두 연산에 대한 평균값입니다.
- 예시, 해시 테이블에 데이터 삽입은 Θ(1) 분할 상환 실행시간이 듭니다.
✔ Karp-Rabin 알고리즘
: 문자열에 해싱 기법을 사용하여 해시 값으로 비교하는 알고리즘입니다.
⁉️ 롤링 해시 ADT
문자열 x가 다음 연산자에 적용됩니다.
- r(): 문자열 x = h(x) 일 때의 해시 값입니다.
- r.append(c): 문자열 x 끝에 문자 c를 넣습니다.
- r.skip(c): 문자열 x의 첫 문자가 c라는 가정 하에 첫 문자를 지웁니다.
# s의 해시 값을 구합니다.
for c in s: rs.append(c)
# t의 첫 s 길이 문자열에서 해시 값을 구합니다.
for c in t[:len(s)]: rt.append(C)
if rs() == rt():
...
for i in range(len(s), len(t)):
rt.skip(t[i-len(s)])
rt.append(t[i])
if rs() == rt(): ...- 해시 값이 같으면 문자열도 같을 수 있으니 s == t[i-len(s)+1:i+1]를 확인합니다.
⇒ 시간은 O(|s|)이 걸립니다. - 확인해서 같다면 짝을 찾은 것입니다. 확인해서 다른 경우는 1/|s|보다 작은 확률로 발생합니다.
⇒ i당 기대 실행시간은 O(1)입니다. - 기대 시간 = O(|s|+|t| + match·|s|)
⁉️ 자료 구조
: 문자열 x를 a진법으로 쓰여진 여러 자릿수의 수 u로 봅니다. a는 알파벳의 크기입니다.
- r() = u mod p, (이상적으로는 무작위) 소수 p ≈|s| 또는 |t| (나누기 방법)
- r은 u가 아닌, u mod p와 |x|(사실 a^(|x|))를 가집니다.
⇒ 작고 빠르게 실행할 수 있습니다.(u mod p는 하나의 기계 단어와 동일) - r.append(c): (u·a + ord(c)) mod p = [(u mod p)·a + ord(c)] mod p
- r.skip(c): [u−ord(c)·(a|u|−1 mod p)] mod p = [(u mod p)−ord(c)·(a|x−1| mod p)] mod p
👀 자료 구조의 내용 부분은 완벽히 이해하지 못하여 강의 자료 내용을 적어두었습니다.
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수1 (0) | 2022.10.31 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 3: 개방 주소법 (0) | 2022.10.27 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 1 (0) | 2022.10.24 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 선형 시간 정렬(정수 정렬) (0) | 2022.10.21 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 균형 이진 탐색 트리 (0) | 2022.10.20 |