BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 단일 시작 단일 도착 다익스트라

: s에서 t까지의 최단 경로만 필요하다면 Q에서 제거되었을 때 알고리즘을 멈춥니다. u=t일 때 종료합니다.
✔ 양방향 탐색

: 여기에서 다루는 속도를 가속화시키는 방법은 최악의 경우 복잡도를 바꾸지 않지만 실제에 적용되었을 때 방문하는 정점의 개수를 줄입니다.

s에서 시작하는 기존의 다익스트라 알고리즘의 첫 번째 단계를 실행해서 순방향으로 경로를 찾습니다. 그리고 t에서부터의 역방향 탐색(간선을 반대로 따라가는 것)을 시작합니다.
df[u] : 전방향 탐색에서의 거리를 저장
db[u] : 역방향 탐색에서의 거리를 저장
Qf : 전방향 탐색에 이용
Qb : 역방향 탐색에 이용
Πf : 기존 구조
Πb : 간선의 반향과 반대 구조
⁉️ 종료 조건은 무엇인가요?
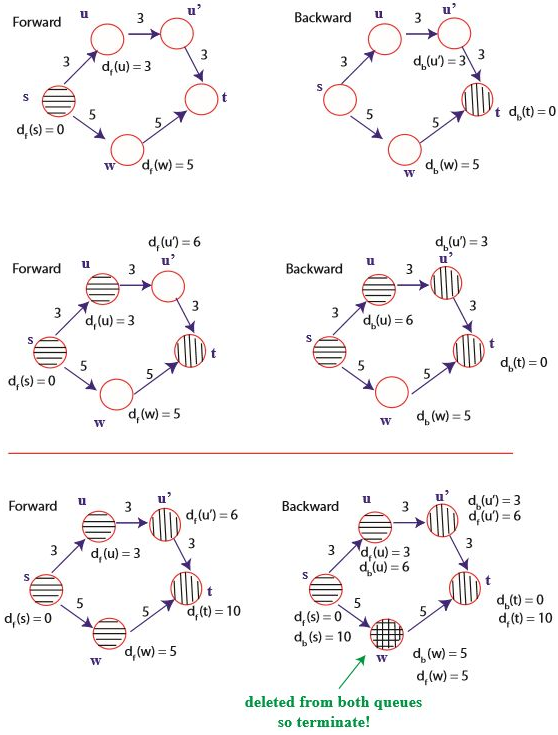
어떤 정점 u가 전방향 탐색과 역방향 탐색 모두에서 처리된 경우입니다. 이 조건은 경계가 만난다는 것을 의미합니다. 즉 전진 탐색과 후진 탐색 모두의 우선순위 큐 Qf와 Qb에서 제거되었을 때 종료합니다.
⁉️ 종료 후에 s에서 t까지의 최단 경로를 어떻게 찾을까요?
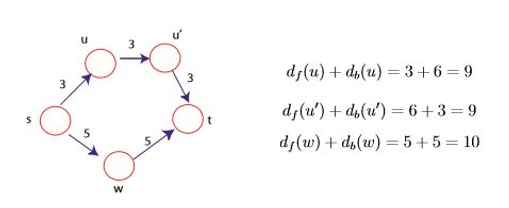
정점 w가 Qf와 Qb 모두에서 추출된 경우 Πf를 이용하여 s에서 w까지의 최단 경로를 구합니다. 이를 s가 나올 때까지 반복합니다. 그리고 난 후에 Πb를 이용하여 최단 경로를 찾습니다.(이 경우는 t부터 w까지의 역방향 경로입니다.)
→ w가 최단 경로에 없는 경우 문제가 발생합니다. 이럴 경우 w와 다를 수 있는 정점 x를 찾되 df[x]+db[x]값이 최소인 정점을 찾습니다. 그리고 Πf를 이용해서 s에서 x까지의 최단 경로를 찾고 Πb를 이용해서 t에서 x까지의 최단 경로를 거꾸로 찾습니다.
✔ 목표지향 탐색 또는 A*
: 간선의 가중치를 수정해서 최단 경로를 찾아가는 것입니다. 정점에 대해 잠재력 함수에 따라 간선의 가중치를 수정합니다.

⁉️ 정확성
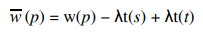
가중치 w(작대기)로 수정된 그래프에서도 최단 경로가 유지됩니다. 다익스트라를 적용하기 위해서 모든 간선 (u, v)에 대해서 w(작대기)(u, v) ≥ 0 를 만족해야 합니다. 적절하고 조건을 만족하는 잠재력 함수를 찾아야 합니다.
⁉️ 랜드마크
그래프의 정점의 부분집합 랜드마크 집합 LCV가 있습니다. 모든 정점 u∈V, l∈L에 대해 δ(u, l)를 미리 계산합니다. 각 랜드마크 l에 대한 잠재력 함수 (λt)^l (u) = δ(u, l) − δ(t, l)입니다.
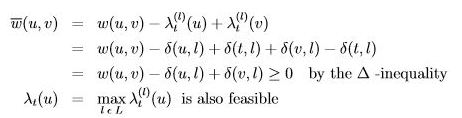
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 2 (2) | 2022.11.15 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 동적 프로그래밍 1 : 메모이제이션, 피보나치 수, 최단 경로, 추측 (0) | 2022.11.14 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 3 : 벨만 포드 (0) | 2022.11.10 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 2 : 다익스트라 (0) | 2022.11.08 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 1 : 도입 (0) | 2022.11.07 |