BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 동적 프로그래밍
* DP ≈ “세심한 무차별 대입법”
* DP ≈ 추측 + 재귀 + 메모이제이션
* DP ≈ 문제를 합리적인 개수의 하위 문제로 나누고 해를 비순환적으로 연관 짓습니다. 보통 해의 일부를 추측합니다.
* time = #subproblems x time/subproblem
→ 근본적으로 분할 상환합니다. 각 하위 문제를 한 번만 셉니다.
→ 메모이제이션을 통해 처음 이후에는 O(1) 시간이 걸립니다.
* DP ≈ DAG에서의 최단 경로
⁉️ 동적 프로그래밍의 "간단한" 5단계
* 반드시 순차적인 것은 아닙니다.
- 하위 문제를 정의합니다. ⇒ 하위 문제의 개수를 셉니다.(#subprobs)
- 해의 일부를 추측합니다. ⇒ 선택지의 개수를 셉니다.(#choices)
- 하위 문제의 해를 연관짓습니다. ⇒ 하위 문제당 시간을 계산합니다.(time/subpr)
- 재귀와 메모이제이션 혹은 DP 테이블을 상향식으로 만듭니다.
⇒ 시간 = 하위 문제당 시간x하위 문제의 개수(total time)
하위 문제가 비순환이고 위상 순서가 있다는 걸 확인합니다. - 기존 문제를 풉니다. - 하위 문제와 같거나 하위 문제의 해를 합쳐서 풉니다.
⇒ 추가 시간이 걸립니다.(extra time)

✔ 글 정렬
글을 "좋은"줄로 나눕니다.
- MS Word/Open Office에서 쓰이는 알고리즘 : 첫 줄에 가능한 많은 단어를 넣고 반복합니다.
→ 좋지 않은 줄을 만들 수 있습니다.

- 단어[i : j]에 대해 "나쁨"을 정의합니다.
총길이가 페이지 너비보다 크면 ∞, 아니면 (페이지 너비 - 총길이)^3
⁉️ 목표
: 단어를 나눠서 "나쁨"의 합을 최소화합니다.

- 하위 문제 : suffix 단어[i : ]의 최소 나쁨
⇒ 하위 문제 개수 = Θ(n), n = 단어 개수 - 추측 : 첫 줄을 어디서 끊을지(i : j)
⇒ 선택지 개수 = n-i = O(n) - 재귀 :
DP(i) = min(DP(j)+ 나쁨(i, j), i+1부터 n+1까지의 모든 j에 대해서 나머지 문제와 첫 줄의 비용의 합)
time/subprob = O(n), DP[n] = 0 - 순서:
i = n, n-1, ..., 1, 0,에 대해 총 시간 = Θ(n^2) - 답 : DP(0)
✔ 부모 포인터
부모 포인터의 아이디어는 어떤 추측이 가장 좋았는지 기억하는 것입니다.
총비용과 실제 해를 찾기 위해 부모 포인터(각 하위 문제에서 어떤 추측이 쓰였는지)를 저장하고 거꾸로 풉니다.
- 보통 최솟/최댓값과 최소/최대 인수를 기억합니다.
- 예제: 글 정렬

- 메모이제이션과 상향식 방법과 같이 이 변환은 자동입니다. ⇒ 생각할 필요 X
✔ 정보를 모두 알고 있는 블랙잭
블랙잭의 경우 카드로 21에 가까운 수를 만들면 이기는 게임입니다.(21 초과 시 지게 됩니다.) 이 게임의 목표는 $1 내기에서 최대한 많이 따는 것으로 카드의 합이 17일 경우 더 이상 카드를 받지 않는 것을 전략으로 세웠습니다.
⁉️ 블랙잭 설정
- 카드 = C0, C1, ... , Cn-1
- 딜러 vs 한 명의 참가자
- $1 내기
⁉️ 진행
1. 하위 문제 개수 = n
2. 추측 : 참가자가 몇 장의 카드를 더 받을 것인지 ⇒ 선택지 개수 ≤ n
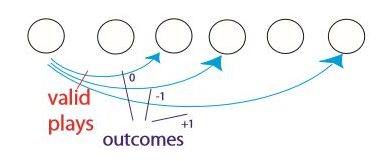
3. 재귀 : BJ(i) = max(결과∈{-1, 0, 1} + BJ(i + 사용된 카드), 21을 넘지 않을 동안 0,1,... 인 받은 카드 개수)
⇒ 하위 문제당 시간 = Θ(n^2)
👀 제공된 자료에 존재
4. 순서 : n부터 0까지 i에 대해
총 시간 = Θ(n^3)

5. 답 : BJ(0)
자세한 재귀 : 메모이제이션 전(나누기와 두 배 걸기 제외할 때)

'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 4 (0) | 2022.11.17 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 3 (0) | 2022.11.16 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 동적 프로그래밍 1 : 메모이제이션, 피보나치 수, 최단 경로, 추측 (0) | 2022.11.14 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 4 : 다익스트라 가속화 (1) | 2022.11.11 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 3 : 벨만 포드 (0) | 2022.11.10 |