728x90
반응형
BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 동적 프로그래밍(DP)
- 강력한 알고리즘 디자인 기법
- 보기에는 지수 시간이 걸리는 많은 문제도 DP를 사용하면 (사용해야지만) 다항 시간에 풀 수 있음
- 특히 최적화 문제(최소화/최대화)에 쓰임(최단 경로 문제)
* DP ≈ “세심한 무차별 대입법”
* DP ≈ 재귀+ 재사용
✔ 피보나치 수

⁉️ 목표
: n번째 피보나치 수를 계산하는 것
⁉️ 단순 알고리즘(재귀 정의)
def fib(n):
if n <= 2:
return 1
else:
return fib(n-1) + fib(n-2)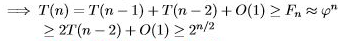
정확하지만 지수 시간이 걸리므로 좋은 알고리즘은 아닙니다.
⁉️ 메모이제이션 DP 알고리즘
memo = {}
def fib(n):
if n in memo:
return memo[n]
else:
if n <= 2:
return 1
else:
memo[n] = fib(n-1) + fib(n-2)
return memo[n]- 모든 k에 대해 fib(k)는 처음 호출될 때만 재귀 호출을 합니다.
- n개의 메모이제이션되지 않은 호출만이 존재합니다.
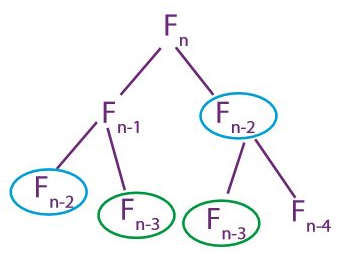
- 메모이제이션된 호출은 Θ(1) 시간이 걸립니다.
→ 재귀를 무시한다면 호출당 Θ(1) 시간이 걸립니다.
* DP ≈ 재귀 + 메모이제이션
- 메모이제이션 (기억하기) & 문제를 푸는데 도움이 되는 하위 문제 해의 재사용
피보나치 수의 하위 문제는 F1, F2, ..., Fn입니다. - 소요 시간 = 하위 문제 개수 · 하위 문제당 소요 시간
피보나치 수: 하위 문제 개수는 n이고, 하위 문제당 소요 시간은 Θ(1) = Θ(n)입니다 (재귀 무시).
⁉️ 상향식 DP 알고리즘
def solve(n):
# ------------------------------------------- Θ(n)
fib = {}
for k in range(1, n+1):
# --------------------------------- Θ(1)
if k <= 2:
f = 1
else:
f = fib[k-1] + fib[k-2]
fib[k] = f
# ---------------------------------------
return fib[n]
# -------------------------------------------------- 메모이제이션 DP와 계산이 정확히 일치합니다.
- 일반적으로 하위 문제 종속 방향성 비순환 그래프의 위상을 정렬합니다.
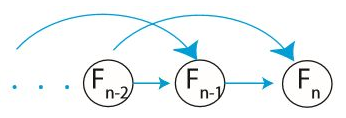
- 재귀가 없기 때문에 사실상 더 빠릅니다.
- 분석이 더 쉽습니다.
- 공간을 아낄 수 있습니다.
👀 자주 사용하는 피보나치 함수
def fibo(n):
x, y = 0, 1
for _ in range(n):
x, y = y, x+y
return x
👀 나눠준 자료와 강의 내용이 뒤섞여 있어 나눠준 자료를 기반으로 정리하였습니다.
✔ 최단 경로

- 재귀적 알고리즘
→ 지수 시간이 걸리므로 좋은 알고리즘이 아닙니다.
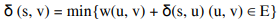
- 메모이제이션 DP 알고리즘
: 순환이 있다면 무한 시간이 걸리게 됩니다. 어떤 경우에는 음수 순환 처리가 필요합니다.
- 방향성 비순환 그래프에서는 O(V+E) 시간이 걸립니다.
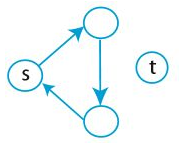
* 하위 문제 종속은 비순환이어야 합니다.
- 하위 문제가 늘어난다면 순환 종속을 없앨 수 있습니다.
: δk(s, v) = k개 이하 간선을 사용한 s에서 v까지의 최단 경로 - 재귀
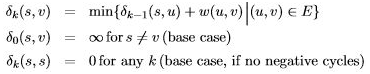
- 목표
: δ(s, v) = δ|V |−1(s, v) (음수 순환이 없는 경우) - 메모이제이션

- 실제로는 δk(s, v)에 대해 Θ(진입차수(v))

✔ 추측

- s에서 v까지의 최단 거리 계산
→ 경로에서는 마지막 간선을 알 수 없기 때문에 (u, v)라고 추측합니다.

- 최선의 추측을 찾기 위해 모든 (|V|)값들을 시도해보고 최적을 찾습니다.
* 비결 : 하위 문제당 적은 (다항) 가능한 추측 - 하위 문제당 시간을 결정하는 요인입니다.
* DP ≈ 재귀 + 메모이제이션 + 추측
⁉️ DAG
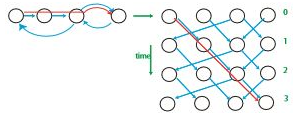
- 시간을 나타내도록 그래프를 복제하는 것과 비슷합니다.
- 그래프의 최단 경로를 방향성 비순환 그래프의 최단 경로로 변환합니다.
* DP ≈ 몇 방향성 비순환 그래프의 최단 경로
반응형
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 3 (0) | 2022.11.16 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘 : 동적 프로그래밍 2 (2) | 2022.11.15 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 4 : 다익스트라 가속화 (1) | 2022.11.11 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 3 : 벨만 포드 (0) | 2022.11.10 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 2 : 다익스트라 (0) | 2022.11.08 |