BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 무리수

: 피타고라스는 정사각형의 대각선의 길이와 한 변의 길이의 비율은 정수비로 표현할 수 없다는 것을 발견했습니다. 따라서 그 비율을 정수로 이루어진 비인 유리수로 표현할 수 없습니다. 그는 이것을 '설명 불가'라고 칭했습니다. 무리수를 위협으로 생각했기 때문에 무리수의 패턴을 찾으려고 시도했습니다. 하지만 결국 패턴을 찾아내지 못했습니다.
→ 고정밀 계산이 필요한 또 하나의 이유가 됩니다.
👀 무리수에 숨겨진 특정한 패턴이 있을까요?
⁉️ 카탈란 수
: 올바른 괄호 구조 문자열로 이루어진 집합 P는 아래와 같이 귀납적으로 정의합니다.
- λ ∈ P
(λ: 빈 문자열) - 만약 α, β ∈ P이면, (α)β ∈ P이다.

이 규칙을 반복적으로 적용해나가면 올바른 괄호 구조 문자열을 계속해서 얻을 수 있습니다. 빈 문자열이 아닌 모든 올바른 괄호 구조 문자열은 특정한 α, β쌍을 이용하여 규칙 2로부터 얻을 수 있습니다. 카탈란 수를 계산하여 나열하고 집합의 원소 개수에 대한 분석적인 형태를 찾는 것입니다.
⁉️ 나열해보기
Cn : n 쌍의 괄호를 가지는 올바른 괄호 구조 문자열의 개수
C0 = 1 빈 문자열
Cn+1: 특정한 규칙2로부터 얻어지는 n+1쌍의 괄호를 가지는 올바른 괄호
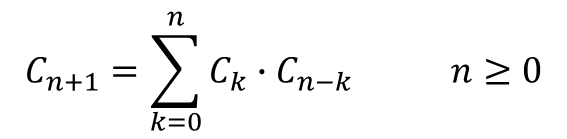
구조의 모든 문자열의 개수
한 쌍의 괄호를 가진 문자열은 규칙2로부터 명확하게 얻어집니다. k쌍의 괄호를 가진 문자열은 α로부터 얻어지고, n−k쌍의 괄호를 가진 문자열은 β로부터 얻어집니다.

✔ 뉴튼 방법
: 연속 근사법을 이용하여 f(x) = 0의 해를 찾는 방법입니다.

점(xi, f(xi))에서의 접선은 y = f(xi) + f'(xi)·(x-xi)이고 f'(xi)는 도함수입니다. xi+1은 x축과의 교점이 됩니다.
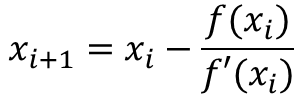
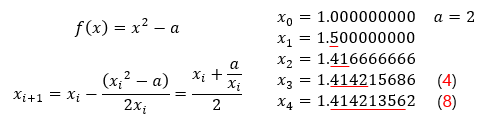
⁉️ 제곱근
: 이차적 수렴은 자릿수의 개수가 두 배로 늘어나는 것을 의미합니다. 따라서 뉴튼 방법을 사용하기 위해서는 고정밀 나눗셈을 계산해야 합니다.
✔ 고정밀도 계산

이렇게 만들어지는 정수는 뉴튼 방법을 적용할 수 있습니다.
⁉️ 고정밀도 곱셈
: 두 개의 n자릿수 숫자를 곱하는 경우 필요합니다.(n은 2진수 또는 10진수, r=2, 10)

절반 크기를 가지는 숫자들을 4번 곱셈으로 계산 ⇒ Θ(n^2), 제곱 시간 알고리즘이 됩니다.
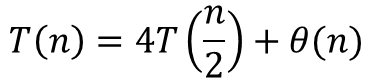
⁉️ 카라추바 알고리즘
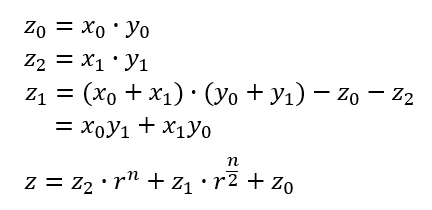
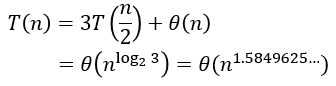
이 방법은 Θ(n^2)보다 짧은 시간에 가능합니다.
⁉️ 흥미로운 기하학 문제

BD=1일 때 AD의 길이는?

뉴튼 방법을 이용하여 수백 자리의 정밀도까지 계산할 경우 카탈란 수가 나오는 것을 볼 수 있습니다.
👀 아래의 부분은 강의에는 없는 제공된 자료물 내용입니다.
⁉️ 추가 설명
실함수 Q의 멱급수에 대해서 알아보겠습니다.

일반적인 선형대수를 이용하면, 아래와 같은 식을 얻을 수 있습니다.


위의 등식이 성립하기 위해서는 Q(x)의 멱급수는 1+Q(x^2)의 멱급수와 완전히 같아야 합니다. 따라서 각 멱급수의 모든 상수가 동일할 때 성립합니다. 따라서, 아래와 같은 경우에 이 등식이 성립합니다.

따라서 함수 Q의 모든 계수는 카탈란 수가 된다는 것을 알 수 있습니다.
2차 방정식을 이용해서 함수 Q를 계산하면 아래와 같습니다.

두 가지 해 중 음의 제곱근을 가지는 해를 이용하면 아래의 값을 얻을 수 있습니다.

함수 Q의 멱급수에 대입하면 아래와 같습니다.

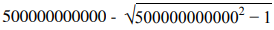
따라서 위에서 보았듯이 24번째 자릿수마다 카탈란 수가 나오게 됩니다.
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 그래프 1 : 너비 우선 탐색 (0) | 2022.11.02 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수2 (0) | 2022.11.01 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 3: 개방 주소법 (0) | 2022.10.27 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 2 (0) | 2022.10.25 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 1 (0) | 2022.10.24 |