728x90
반응형
BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 그래프 탐색
그래프 탐색은 "그래프를 탐험하다"는 것이라고 할 수 있습니다. 그래프를 탐색하는데 여러 가지 개념들이 있습니다.
- 시작 점 s에서 원하는 정점으로의 경로를 찾는 것
- 그래프의 또는 s에서 도달할 수 있는 모든 정점과 간선을 방문하는 것
⁉️ 그래프 : G = (V, E)

- V = 정점의 집합(임의의 레이블)
- E = 간선의 집합, 정점의 쌍(v, w)
- 순서쌍 ⇒ 그래프의 방향이 있는 간선
- 비순서쌍 ⇒ 무방향
⁉️ 응용
- 웹크롤링(구글이 페이지를 찾는 방법)
- 소셜 네트워킹(페이스북이 친구 찾기를 사용하는 법)
- 네트워크 브로드캐스트 라우팅
- 가비지 컬렉션
- 모델 검사(무한 상태 기계)
- 수학적 추측 확인하기
- 퍼즐이나 게임 풀기
✔ 포켓 큐브: 2x2x2 루빅큐브

⁉️ 짜임새 그래프 또는 짜임새 공간
- 가능한 각 상태에 대한 정점
정점의 개수 : 8! ·3^(8) = 264, 539, 520
8! 은 임의의 위치에서의 8개의 큐브릿을 의미하고 3^(8)은 각각의 큐브릿을 세 번 돌릴 수 있다는 것을 의미합니다. - 한 상태에서 다른 상태로의 기본 이동에 대한 간선(예: 90도 회전)
- 무방향: 거꾸로 움직일 수 있음
⁉️ 지름("신의 숫자")
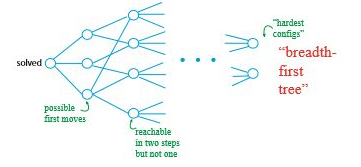

2x2x2의 경우 11, 3x3x3의 경우 20, nxnxn의 경우 Θ(n^2/lgn)입니다. 만약 큐브의 대칭성을 없애면 24개 나눌 수 있고 실제로 도달할 수 있는 곳을 생각하면 3으로 또 나눠줄 수 있습니다.(3개의 연결된 구성 요소가 있습니다.)
✔ 그래프 표현: (자료구조)
⁉️ 인접 리스트
: |V| 연결 리스트의 배열 Adj
- 각 정점 u∈V에 대해, Adj[u]는 u의 이웃들을 저장합니다.
예: {v∈V | (u, v)∈E}. 방향 그래프에서 (u, v)는 나가는 간선입니다.
Adj(u)는 함수입니다. → 로컬 구조를 계산합니다. "제로" 공간이 필요합니다.

- 파이썬
: Adj = 리스트/집합 값의 딕셔너리;
정점 = 해시 가능한 것(예: int, tuple) - 장점
: 같은 정점에 여러 그래프가 있을 수 있습니다.
⁉️ 객체 지향 변형
- 각 정점 u에 대한 객체
- u.neighbors = 이웃한 점들의 리스트(예: Adj[u])
즉, 이것은 묵시적으로 표현된 그래프를 위한 방법입니다.
⁉️ 입력 목록
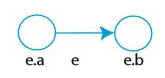
- 간선도 객체로 만들 수 있다
- u.edges = u에서 (나가는) 간선의 리스트
- 장점
: 해싱 없이도 간선을 저장할 수 있습니다.
✔ 너비 우선 탐색(Breadth-First Search)
- 목표는 주어진 정점 s에서 도달할 수 있는 모든 정점을 탐색하는 것입니다.
- O(V+E) 시간
- s에서 레벨별로 그래프를 탐색합니다.
level 0 = {s}
level i = 최소 i개의 간선의 경로로 도달할 수 있는 정점
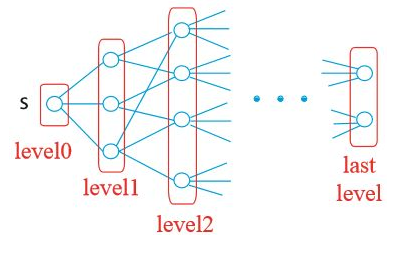
- 모든 나가는 간선을 사용해 level i-1에서 level i > 0를 만듭니다. 하지만 이전 level의 정점은 무시합니다.
⁉️ 너비 우선 탐색의 알고리즘
def BFS(V, Adj, s):
level = {s:0}
parent = {s:None}
i = 1
frontier = [s]
while frontier:
next = []
for u in frontier:
for v in Adj[u]:
if v not in level:
level[v] = i
parent[v] = u
next.append(v)
frontier = next
i += 1
⁉️ 예시

⁉️ 분석
- 정점 V가 next를 (다음으로 frontier를) 한 번만 방문합니다.(level[v]가 정의되므로)
기본 경우: v=s - Adj[v]는 루프를 한 번만 통과합니다.

- O(E) 시간
- O(V+E)("선형 시간") v에서 도달할 수 없는 정점을 리스트합니다.(level이 지정되지 않은 정점)
⁉️ 최단 경로
- 각 정점 v에 대해 s에서 v로 갈 수 있는 가장 적은 수의 간선은 아래와 같습니다.

- 부모 포인터는 최단 경로 트리를 형성한다 = 각 v에 대한 최단 경로의 조합
⇒ 최단 경로를 찾으려면 v를 찾고, parent[v]를 찾고, parent[parent[v]]를 찾아 s에 도달하거나 끝날 때까지 찾습니다.
반응형
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 1 : 도입 (0) | 2022.11.07 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 그래프 2 : 깊이 우선 탐색 (0) | 2022.11.04 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수2 (0) | 2022.11.01 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수1 (0) | 2022.10.31 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 3: 개방 주소법 (0) | 2022.10.27 |