BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 복습
√2 를 백만 자릿수까지 계산

|√a|를 뉴튼 방법을 이용하여 계산

위의 결과들이 실제로 이차적 수렴의 성질인지 알아보기 위하여 뉴턴법의 오차를 살펴보겠습니다.
✔ 뉴턴법의 오차 분석


전체적으로 보았을 때 알 수 있는 것은 오차에 대한 아래의 식입니다.

분모 부분의 (1+εn)에서 n이 계속해서 커질수록 εn은 예상했던 대로 0에 가까워집니다. 그래서 (1+εn) 값은 1이라고 할 수 있고 결국 오차값이 이차적 수렴의 성질을 가진다고 할 수 있는 것입니다. 굉장히 작은 값이지만 매 반복마다 제곱값으로 작아지는 것입니다. 만약 0.01이 가장 처음의 εn 값이라고 한다면 (εn)^2은 0.0001이 되는 것입니다.
✔ 곱셈 알고리즘
👀 제공된 자료에는 강의에서 사용된 n이 d로 나와있습니다.
1. 기본 분할 정복 알고리즘

2. 카라추바 알고리즘

3. Toom-Cook 알고리즘
카라추바 알고리즘을 일반화(k ≥ 2 인 k 부분으로 쪼개는 경우)
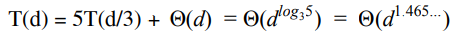
4. Schönhage-Strassen
거의 선형 시간에 가깝고 Θ(d lgd lglgd) 시간입니다. 이 방법은 FFT(고속 푸리에 변환)을 사용합니다. 여기까지는 모두 gmpy 패키지에 구현되어 있습니다.
5. Furer (2007)

log*n은 반복 로그라고 부르는데, 로그값의 결과가 1보다 작거나 같을 때까지 반복해서 로그를 계산해야 하는 횟수를 의미합니다.
✔ 고정밀 나눗셈
a/b 의 고정밀 표현을 계산해야 하는 경우
- 1/b의 고정밀 표현을 먼저 계산합니다.
- 1/b의 고정밀 표현은 R이 큰 값인 경우에 [R/b]을 R로 나눈 결과라고 할 수 있습니다.
예) R=2^k인 경우 2진수의 나눗셈을 쉽게 할 수 있습니다.
⁉ R/b을 계산하기 위한 뉴튼 방법

⁉ 예시

→ 나눗셈은 O(lgn n^a)이 됩니다.
⁉ 오차 분석

각 단계마다 자릿수가 두 배로 증가하므로 이차적 수렴입니다.
👀 제공된 자료 내용
나눗셈의 복잡도는 lg d에 곱셈의 복잡도를 곱한 값이라고 생각할 수 있습니다. lg d는 d 자릿수 정확도를 만들기 위해서 필요한 곱셈의 반복 횟수이기 때문입니다. 하지만 실제로는 나눗셈의 복잡도는 곱셈의 복잡도와 동일합니다. 먼저 α ≥ 1에 대해서 n 자릿수 곱셈의 복잡도를 Θ(n^α)이라고 한다면, 나눗셈은 각 반복마다 다른 크기의 자릿수를 가지는 숫자를 곱하는 것을 필요로 합니다.

초기에는 작은 자릿수의 숫자를 계산하지만, 갈수록 그 숫자는 길어져서 d 자릿수를 계산하게 됩니다. 따라서 나눗셈에 사용되는 연산의 횟수를 계산하면 다음과 같은 형태가 됩니다.
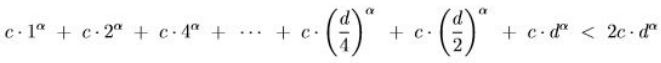
✔ 제곱근 계산의 복잡도
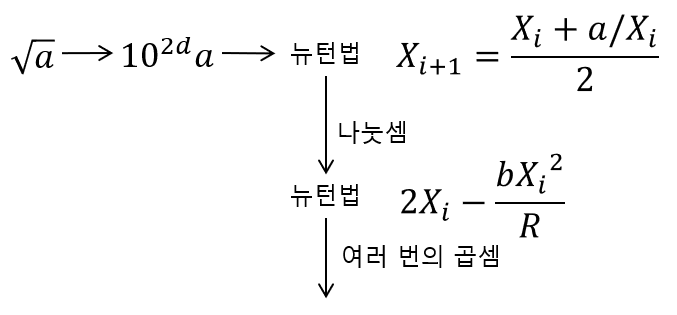
제곱근을 계산할 때의 복잡도는 나눗셈을 할 때의 복잡도와 같고 이것은 결국 곱셈의 복잡도와 같다는 것입니다.
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 그래프 2 : 깊이 우선 탐색 (0) | 2022.11.04 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 그래프 1 : 너비 우선 탐색 (0) | 2022.11.02 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수1 (0) | 2022.10.31 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 3: 개방 주소법 (0) | 2022.10.27 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 해싱 2 (0) | 2022.10.25 |