728x90
반응형
BoostCourse의 "[MIT]파이썬을 이용한 알고리즘의 이해" 강의 내용을 정리한 글입니다.
✔ 복습
- 그래프 탐색 : 그래프를 탐험하는 것
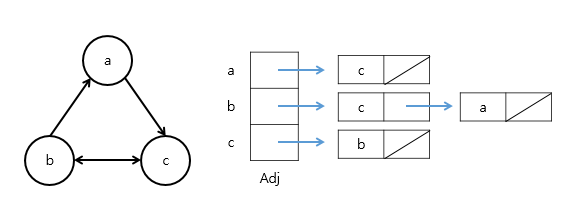
예) 시작점 s에서 원하는 정점까지 가는 경로를 찾는 것 - 인접 리스트 : |V|연결 리스트의 배열 Adj
각 정점 u∈V에 대해, Adj[u]는 u의 이웃들을 저장
예) {v∈V | (u, v)∈E}(방향 그래프에서 (u, v)는 나가는 간선입니다.) - 너비 우선 탐색(BFS)
: s에서 레벨별로 그래프를 탐색합니다. - 최단 경로를 찾습니다.
✔ 깊이 우선 탐색(DFS)
: 그래프를 재귀적으로 탐색하고 필요에 따라 역추적하여 미로를 해결하려는 것과 같습니다. 깊이 우선 탐색에서 주의할 점은 정점을 반복하지 않는 것입니다.
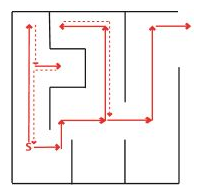
⁉️ 깊이 우선 탐색 알고리즘
parnet = {s: None}
def DFS_visit(V, Adj, s):
for v in Adj[s]:
if v not in parent:
parent[v] = s
DFS_visit(V, Adj, v)
def DFS(V, Adj):
parent = {}
for s in V:
if s not in parent:
parent[s] = None
DFS_visit(V, ADj, s)
⁉️ 예시

⁉️ 분석
- 깊이 우선 탐색의 재귀를 고려하지 않는다면 O(V)가 되지만 마지막 인수인 V의 깊이 우선 탐색 방문은 최대 한 번, 정점 V당 한 번 호출됩니다. 또한 그 정점 V에 대한 인접 리스트의 길이도 고려해야 합니다.
⇒ 모든 정점의 인접 리스트 V의 길이에 대한 합계
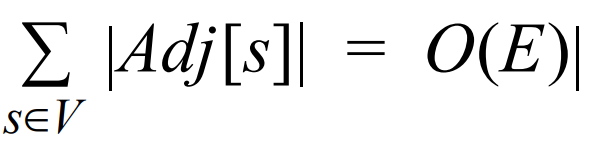
⇒ 최종 시간 : O(V+E) 시간 (선형 시간)
⁉️ 간선 분류
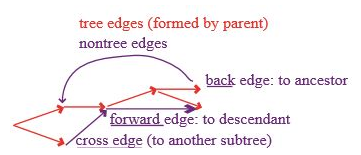
- 트리 간선
: 부모 포인터가 명시하고 있는 것입니다. 이 간선을 통해 새로운 정점을 방문하게 됩니다. - 순방향 간선
: 정점에서 자손으로 가는 간선입니다. - 역방향 간선
: 정점에서 조상으로 가는 간선입니다. - 교차 간선
: 선조 관계가 아닌 두 하위 트리 또는 정점 사이의 간선입니다.
👀 무방향 그래프에서는 트리 간선과 역방향 간선만 있습니다.
✔ 순환 검출
그래프 G는 순환이 존재 ⇔ 깊이 우선 탐색은 역방향 간선이 존재
⁉️ 증명

- vi 방문이 끝나기 전, vi+1을 방문하고 끝낼 것입니다.
: (vi, vi+1) 간선을 고려합니다. ⇒ vi+1을 지금 방문하거나 이미 방문했을 것입니다. - v0 방문이 끝나기 전, vk를 전에 방문한 적이 없다면 방문할 것입니다.
- vk(또는 v0) 방문이 끝나기 전, (vk, v0) 간선을 역방향 간선으로 볼 것입니다.
✔ 위상 정렬
: 그래프의 정점을 정렬하는것입니다. 그리고 이는 깊이 우선 탐색을 실행하고 결과는 정점의 마무리 시간이 역순으로 나옵니다. 이는 그래프의 모든 정점을 방문해야 하는 또 다른 응용입니다.
⁉️ 잡 스케줄링
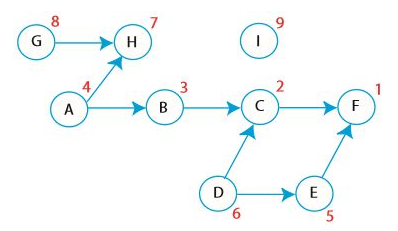
주어진 비순환성 방향 그래프(DAG)에서 모든 간선이 낮은 레벨에서 높은 레벨을 가리킬 수 있도록 정점을 순서대로 정렬합니다. 여기서는 정점들이 해야 할 일을 나타내는 것이고 간선은 의존 상태를 의미할 때 의존 상태를 위반하지 않고 할 일을 정렬합니다.
⁉️ 정확성
이전 수에서 이후 수를 가리킨다고 증명하고 싶을 때, 어떤 간선 (u, v)에 대해서 u는 v 이전에 정렬됩니다.

- 만약 v 전에 u가 방문되면 :
- u 방문이 끝나기 전, v를 방문할 것입니다.((u, v)를 통하거나 다른 방법을 통해)
- u 전에 v가 끝납니다.
- 만약 u 전에 v가 방문되면 :
- 그래프는 비순환적입니다.
- v에서 u로 도달할 수 없습니다.
- u를 방문하기 전에 v 방문이 끝납니다.
반응형
'프로그램 개발 > 미분류' 카테고리의 다른 글
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 2 : 다익스트라 (0) | 2022.11.08 |
|---|---|
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 최단 경로 1 : 도입 (0) | 2022.11.07 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 그래프 1 : 너비 우선 탐색 (0) | 2022.11.02 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수2 (0) | 2022.11.01 |
| [MIT] 파이썬을 이용한 알고리즘의 이해 - 수1 (0) | 2022.10.31 |